BILANGAN
a. Bilangan bulat adalah himpunan bilangan bulat negatif, bilangan nol dan bilangan bulat positif. Contoh : …., -3, -2, -1, 0, 1, 2, 3, …
b. Bilangan Negatif adalah suatu bilangan yang mempunyai nilai minus (-) atau negatif. Contoh: { -5, -4, -3, -2, -1 dan seterusnya}
c. Bilangan bulat positif adalah suatu bilangan yang mempunyai nilai positif. Contoh: 1,2,3,4,... dan seterusnya)
d. Bilangan Nol adalah satu angka untuk mewakili. Peranan terpenting angka 0 adalah menjadi identitas untuk bilangan real, bulat, dan perhitungan matematika yang lain
e. Bilangan Cacah terdiri atas bilangan bulat positif yang diawali dari bilangan nol. Biasanya bilangan cacah dinotasikan dengan huruf C. Misalnya: C = 0, 1, 2, 3, 4…
f. Bilangan Ganjil terdiri atas bilangan yang tidak dapat habis dibagi dua. Bilangan ganjil dinotasikan dengan huruf J. Misalnya: 1, 3, 5, 7, …
g. Bilangan Genap adalah bilangan yang akan habis jika dibagi dua. Bilangan genap dinotasikan dengan huruf G. Misalnya: G= 2, 4, 6, 8, …
h. Bilangan Prima adalah bilangan yang hanya memiliki dua faktor, yaitu bilangan 1 dan bilangan itu sendiri. Bilangan prima dinotasikan dengan huruf P. Misalnya: 2, 3, 5, 7, 11, …
b. Bilangan Negatif adalah suatu bilangan yang mempunyai nilai minus (-) atau negatif. Contoh: { -5, -4, -3, -2, -1 dan seterusnya}
c. Bilangan bulat positif adalah suatu bilangan yang mempunyai nilai positif. Contoh: 1,2,3,4,... dan seterusnya)
d. Bilangan Nol adalah satu angka untuk mewakili. Peranan terpenting angka 0 adalah menjadi identitas untuk bilangan real, bulat, dan perhitungan matematika yang lain
e. Bilangan Cacah terdiri atas bilangan bulat positif yang diawali dari bilangan nol. Biasanya bilangan cacah dinotasikan dengan huruf C. Misalnya: C = 0, 1, 2, 3, 4…
f. Bilangan Ganjil terdiri atas bilangan yang tidak dapat habis dibagi dua. Bilangan ganjil dinotasikan dengan huruf J. Misalnya: 1, 3, 5, 7, …
g. Bilangan Genap adalah bilangan yang akan habis jika dibagi dua. Bilangan genap dinotasikan dengan huruf G. Misalnya: G= 2, 4, 6, 8, …
h. Bilangan Prima adalah bilangan yang hanya memiliki dua faktor, yaitu bilangan 1 dan bilangan itu sendiri. Bilangan prima dinotasikan dengan huruf P. Misalnya: 2, 3, 5, 7, 11, …
Pada dasarnya pecahan berdasarkan bentuknya dikelompokkan menjadi pecahan biasa, campuran, desimal, dan persen. Pembahasan kali ini akan dimulai dari materi pengenalan pecahan, serta contoh bentuk-bentuk pecahan.
Penjumlahan Pecahan Biasa dan Pecahan campuran
Pecahan biasa adalah pecahan yang terdiri dari pembilang dan penyebut.
Pecahan campuran adalah bilangan yang terdiri dari bilangan bulat dan pecahan sekaligus.
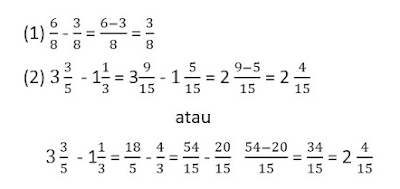
Di bawah ini adalah contoh penjumlahan pecahan biasa berpenyebut sama dan penjumlahan pecahan campuran dengan penyebut berbeda.
CONTOH:
Pengurangan Pecahan Biasa dan Pecahan campuran
Di bawah ini adalah contoh pengurangan pecahan biasa berpenyebut sama dan penjumlahan pecahan campuran dengan penyebut berbeda.
CONTOH:
Penjumlahan dan Pengurangan Pecahan Desimal
Menjumlahkan dan mengurangkan pecahan desimal dapat dilakukan dengan cara bersusun, tanda koma diletakkan sejajar seperti menjumlahkan dan mengurangkan bilangan bulat biasanya.
CONTOH:
Penjumlahan dan Pengurangan Persen
Di bawah ini adalah contoh penjumlahan dan pengurangan persen. Menjumlahkan dan mengurangkan persen bisa dilakukan dengan cara bersusun seperti menjumlahkan dan mengurangkan bilangan bulat
CONTOH:
Perkalian Pecahan Biasa dan Pecahan Campuran
Untuk perkalian pecahan, pengerjaannya lebih mudah. Perkalian pada pecahan diperoleh dengan mengalikan pembilang dengan pembilang dan penyebut dengan penyebut
CONTOH:
CONTOH:
Perkalian Pecahan Desimal
Perkalian pecahan desimal diperoleh dengan mengubah pecahan desimal menjadi pecahan biasa.
ingat:
1 angka dibelakang koma: per 10 (4,5 adalah contoh 1 angka dibelakang koma)
2 angka dibelakang koma: per 100 (0,25 adalah contoh 2 angka dibelakang koma)
CONTOH:
Pembagian Pecahan Biasa dan Pecahan campuran
Untuk pembagian pecahan diperoleh dengan mengalikan pecahan tersebut dengan kebalikan dari pecahan yang lain.
CONTOH:
pada soal pecahan campuran, terlebih dahulu diubah menjadi pecahan biasa kemudian dibalik dan dikalikan. perhatikan contoh soal sebelumnya yang berada diatas, cara mengubah pecahan campuran menjadi pecahan biasa.
Pembagian Pecahan Desimal
Pembagian pecahan desimal diperoleh dengan cara mengubah pecahan desimal menjadi pecahan biasa. perhatikan kembali cara mengerjakan soal pecahan biasa diatas.

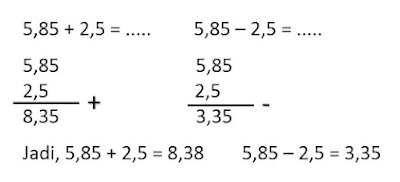



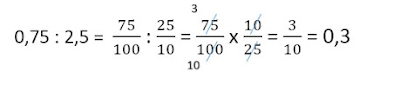
Tidak ada komentar:
Posting Komentar